Everyday Science: Two-Second Rule

by Ryan Gross and Caleb Wehling

Most of us, in that terrifying coming-of-age experience known as “driver’s education,” learned about the two-second rule. For those of you who missed your instructor’s explanation of the two-second rule over the screams of your backseat passengers as you narrowly avoided that tree you still swear came out of nowhere, here’s a reminder: when following another car, keep two seconds of distance between yourself and the car ahead.

To find this distance, we are told to find to some object on the side of the road and, after the car ahead passes the object, count two seconds. If you pass the object within two seconds, you’re too close. Pretty simple, provided you remember to look ahead once in awhile during your calculations to make sure those other roadside objects (people, cars, deer, flying watermelon from that sixth grader’s science project) don’t come out of nowhere.

At high speeds, two seconds between cars corresponds to a longer distance between cars than the distance between cars at low speeds, so the two-second rule seems to hold for all speeds, right? Wrong.

We calculated the time needed between two cars to allow the trailing car enough distance to come to a complete stop before hitting the leading car that had to stop immediately.

Given a braking distance of 57 feet (according to the Iowa Department of Transportation) when traveling at 30 miles per hour (30 mph = 44 feet/second), you need to have 1.3 seconds between you and the car ahead of you: 57 feet needed to stop 44 feet/second=1.3 seconds.

But, of course, our brains need time to process information, cry for our mothers, decide to brake and signal our feet to slam on the brakes. Using an average reaction time of 0.0000000000475 millennia (or 1.5 seconds given by the Iowa Department of Transportation), the total time needed to stop is: 1.3 seconds (braking time) + 1.5 seconds (reaction time)=2.8 seconds total, which doesn’t seem so far off. But at 60 mph, the time needed between vehicles comes out to over four seconds.

So why doesn’t the two-second rule work? The reason is that the energy required to stop is dependent on the force of friction (F) over a distance (x) (W = FΔx) and is also equal to the change in kinetic energy, which is dependent on the mass (m) and speed (v) (ΔKE = ½mv²), which means that FΔx=12mv².

If we double the speed (v), the distance (x) is quadrupled (2² = 4), meaning more stopping distance is necessary at high speeds than predicted by the two-seconds rule. Here’s a graph showing time vs. speed.

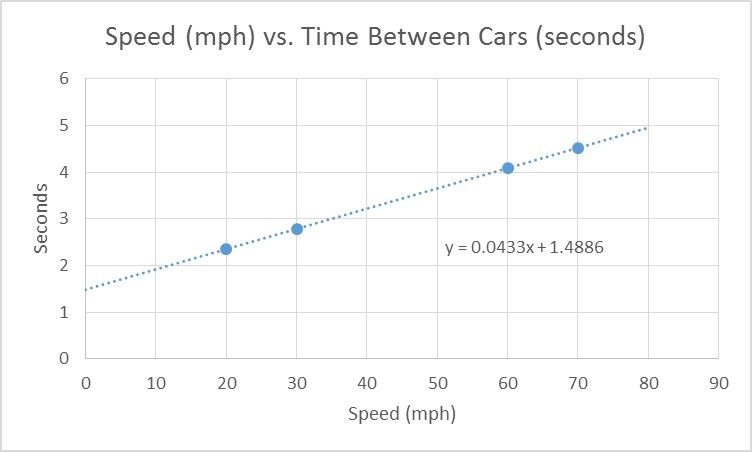
A good approximation would be to add a second to your reaction speed (1.5 seconds) between cars for every 20 mph. If that’s too much math, shoot for about three seconds for city traffic and four to five seconds for highway traffic. Let’s help out those poor driver’s ed students.